Ángulos entre paralelas
De Wikipedia, la enciclopedia libre
En geometría euclidiana, los ángulos entre paralelas son los ocho ángulos formados por dos rectas paralelas y una transversal a ellas. Se clasifican según su congruencia.
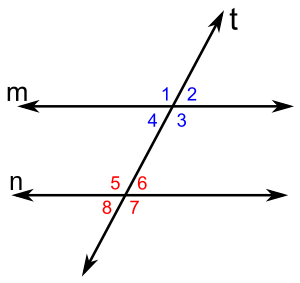 Figura 1: Rectas paralelas m y n, recta transversal t.
Las parejas de ángulos: <1 y <5; <2 y <6; <4 y <8; <3 y <7 se llaman ángulos correspondientes, y son congruentes (figura 1).
Figura 1: Rectas paralelas m y n, recta transversal t.
Las parejas de ángulos: <1 y <5; <2 y <6; <4 y <8; <3 y <7 se llaman ángulos correspondientes, y son congruentes (figura 1).
 Figura 2: Rectas paralelas a y b, transversal t, ángulos adyacentes β y θ.
Figura 2: Rectas paralelas a y b, transversal t, ángulos adyacentes β y θ.
 La relación entre dos rectas paralelas cortadas por una secante es un análisis clásico de la geometría euclidiana, que permite analizar una infinidad de problemas prácticos, así como definir algunos conceptos de interés en cuanto a congruencia y suplementaridad de ángulos.
La relación entre dos rectas paralelas cortadas por una secante es un análisis clásico de la geometría euclidiana, que permite analizar una infinidad de problemas prácticos, así como definir algunos conceptos de interés en cuanto a congruencia y suplementaridad de ángulos.
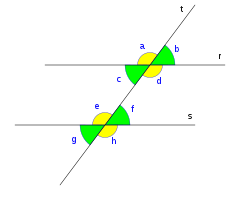 Partiendo de dos rectas paralelas r y s, y una transversal t que corta a ambas, da lugar a ocho ángulos,[1] cuya posición relativa da lugar a su definición.[2]
Partiendo de dos rectas paralelas r y s, y una transversal t que corta a ambas, da lugar a ocho ángulos,[1] cuya posición relativa da lugar a su definición.[2]
Los ángulos adyacentes son suplementarios.(suman 180°)
Los ángulos opuestos por el vértice son congruentes, es decir tienen la misma medida a cada lado del vértice.
Los ángulos alternos internos son congruentes.
Los ángulos alternos externos son congruentes.
Los ángulos colaterales internos son suplementarios.(suman 180°)
Los ángulos colaterales externos son suplementarios.(suman 180°)
Los ángulos correspondientes son congruentes.


Congruencia de triángulos


































Ángulos correspondientes

Ángulos alternos
Son los que "fuera" de las paralelas fueran a distinto lado de ellas y a distinto lado de la transversal. Son iguales entre sí; es decir miden lo mismo.Alternos externos
Las parejas de ángulos: <1 y <7; <2 y <8 se llaman ángulos alternos externos, y son congruentes (figura 1).Alternos internos
Las parejas de ángulos: <4 y <6; <3 y <5 se llaman ángulos alternos internos, y son congruentes (figura 1).Ángulos congruentes entre paralelas
Los ángulos opuestos por el vértice son congruentes, de modo que, de los ocho ángulos formados entre dos paralelas y una transversal, hay únicamente dos distintos, que son adyacentes (figura 2).
Rectas paralelas cortadas por una secante

Descripción

Denominación de los ángulos
- Ángulos adyacentes: Son los angulos que tienen un lado en común y sus otros dos lados son semirrectas opuestas.
Los ángulos adyacentes son suplementarios.(suman 180°)
- Ángulos opuestos por el vértice: Si los lados de uno son semirrectas opuestas a los lados del otro.
Los ángulos opuestos por el vértice son congruentes, es decir tienen la misma medida a cada lado del vértice.
- Ángulos alternos internos: Son los que se encuentran a distinto lado de la secante y en la zona interior de las rectas paralelas.
Los ángulos alternos internos son congruentes.
- Ángulos alternos externos: Son los que se encuentran a distinto lado de la secante y en la zona externa de las rectas paralelas.
Los ángulos alternos externos son congruentes.
- Ángulos colaterales internos: Son los que se encuentran del mismo lado de la secante y entre de las rectas.
Los ángulos colaterales internos son suplementarios.(suman 180°)
- Ángulos colaterales externos: Son los que se encuentran en uno y otro lado de la secante.
Los ángulos colaterales externos son suplementarios.(suman 180°)
- Ángulos correspondientes u homólogos: Son los que se encuentran en el mismo lado de la secante, un ángulo en la parte interior y otro en el exterior de las paralelas.
Los ángulos correspondientes son congruentes.
Teorema para ángulos internos de un triángulo:
Los ángulos internos de todo triángulo suman 180°.

Teorema para ángulos externos de un triángulo:
Un ángulo externo de un triángulo es igual a la suma de los ángulos internos no adyacentes.

CONGRUENCIA Y SEMEJANZA DE TRIANGULOS
Congruencia de triángulos
En matemáticas, dos figuras de puntos son congruentes si tienen los lados iguales y el mismo tamaño (o también, están relacionados por un movimiento) si existe una isometría que los relaciona: una transformación que es combinación de translaciones, rotaciones y reflexiones. Por así decirlo, dos figuras son congruentes si tienen la misma forma y tamaño, aunque su posición u orientación sean distintas. Las partes coincidentes de las figuras congruentes se llaman homólogas o correspondientes.
Criterios de semejanza de triangulos
Los criterios de congruencia de triángulos nos dicen que no es necesario verificar la congruencia de los 6 pares de elementos ( 3 pares de lados y 3 pares de ángulos), bajo ciertas condiciones, podemos verificar la congruencia de tres pares de elementos.
Primer criterio de congruencia: LLL
Dos triángulos son congruentes si sus tres lados son respectivamente iguales.
a ≡ a’
b ≡ b’
c ≡ c’
→ triáng ABC ≡ triáng A’B'C’
Dos triángulos son congruentes si sus tres lados son respectivamente iguales.
a ≡ a’
b ≡ b’
c ≡ c’
→ triáng ABC ≡ triáng A’B'C’
Segundo criterio de congruencia: LAL
Dos triángulos son congruentes si son respectivamente iguales dos de sus lados y el ángulo comprendido entre ellos.
b ≡ b’
c ≡ c’
α ≡ α’
→ triáng ABC ≡ triáng A’B'C’
Dos triángulos son congruentes si son respectivamente iguales dos de sus lados y el ángulo comprendido entre ellos.
b ≡ b’
c ≡ c’
α ≡ α’
→ triáng ABC ≡ triáng A’B'C’
Tercer criterio de congruencia: ALA
Dos triángulos son congruentes si tienen un lado congruente y los ángulos con vértice en los extremos de dicho lado también congruentes. A estos ángulos se los llama adyacentes al lado.
b ≡ b’
α ≡ α’
β ≡ β’
→ triáng ABC ≡ triáng A’B'C’
Dos triángulos son congruentes si tienen un lado congruente y los ángulos con vértice en los extremos de dicho lado también congruentes. A estos ángulos se los llama adyacentes al lado.
b ≡ b’
α ≡ α’
β ≡ β’
→ triáng ABC ≡ triáng A’B'C’
Cuarto criterio de congruencia: LLA
Dos triángulos son congruentes si tienen dos lados respectivamente congruentes y los ángulos opuestos al mayor de los lados también son congruentes.
a ≡ a’
b ≡ b’
β ≡ β’
→ triáng ABC ≡ triáng A’B'C’
a ≡ a’
b ≡ b’
β ≡ β’
→ triáng ABC ≡ triáng A’B'C’
Semejanza de Triángulos:
necesariamente de igual tamaño.
Una semejanza, es un coaguló geométrico difundido de rotación (una rotación y una posible reflexión o simetría axial). En la rotación se pueden cambiar los lados y la radiación de una materia pero no se altera su coagulo.
En el caso del triángulo, la forma sólo depende de sus ángulos (no así en el caso de un rectángulo, por ejemplo, donde uno de sus ángulos es recto pero cuya forma puede ser más o menos alargada, es decir que depende del cociente base / altura).
Se puede simplificar así la definición: dos triángulos son semejantes si sus ángulos son iguales dos a dos.
En la figura, los ángulos correspondientes son A = A', B = B' y C = C'. Para denotar que dos triángulos ABC y DEF son semejantes se escribe ABC ~ DEF, donde el orden indica la correspondencia entre los ángulos: A, B y C se corresponden con D, E y F, respectivamente.
Una similitud tiene la propiedad (que la caracteriza) de multiplicar todas la longitudes por un mismo factor. Por lo tanto las razones longitud imagen / longitud origen son todas iguales, lo que da una segunda caracterización de los triángulos semejantes:
Dos triángulos son semejantes si las razones de los lados correspondientes son congruentes.
Criterios de semejanza de triángulos.
1.-Dos triángulos son semejantes si tienen dos ángulos iguales.
|
2.-Dos triángulos son semejantes si tienen dos lados proporcionales e igual el ángulo que forman.
|
3.- Dos triángulos son semejante si sus lados son proporcionales.
|
Para que dos triángulos sean semejantes es suficiente con que se verifique una de las siguientes condiciones:
1. Dos triángulos son semejantes si tienen dos ángulos respectivamente iguales:
2. Dos triángulos son semejantes si tienen los lados proporcionales:
3. Dos triángulos son semejantes si tienen dos lados proporcionales e igual el ángulo comprendido:
Teorema de Thales
Si dos rectas cuales quieras se cortan por varias rectas paralelas, los segmentos determinados en una de las rectas son proporcionales a los segmentos correspondientes en la otra.


El teorema de Thales en un triángulo
Dado un triángulo ABC, si se traza un segmento paralelo, B'C', a uno de los lados del triangulo, se obtiene otro triángulo AB'C', cuyos sus lados son proporcionales a los del triángulo ABC.


Teoremas de triángulos rectángulos
Teorema del cateto



Teorema la altura


Teorema de Pitágoras




Aplicaciones del teorema de Pitagoras
Altura del triángulo equilátero


Lado de un triángulo equilátero inscrito


Diagonal del cuadrado


Lado de un cuadrado inscrito


Diagonal del rectángulo


Lado oblicuo del trapecio rectángulo



Altura del trapecio isósceles



Apotema de un polígono regular


Apotema del hexágono inscrito








Coin Casino UK » Review and Bonus Codes 2021
ResponderBorrarBest Bitcoin Casino Bonus Codes 2021. Casino is a great choice for UK players. They febcasino offer a wide range of payment 인카지노 methods, Number of games: 1000+Welcome Bonus: 100% up to หาเงินออนไลน์ £200 + 100 Free SpinsWelcome Bonus: 100% up to £200 + 100 Free Spins Rating: 5 · Review by CasinoRewards
Harrah's Cherokee Casino & Hotel - MapYRO
ResponderBorrarHarrah's Cherokee Casino & 아산 출장샵 Hotel 용인 출장안마 is 청주 출장마사지 located in 삼척 출장마사지 Cherokee, North Carolina. The casino hotel in the 충청남도 출장마사지 Harrah's Cherokee Valley River is a 3-minute walk